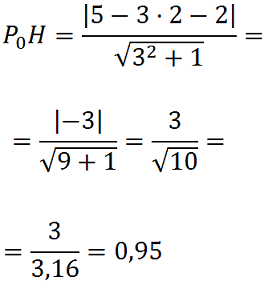Nella lezione precedente abbiamo visto che possiamo calcolare la DISTANZA di un PUNTO da una RETTA applicando la formula: 

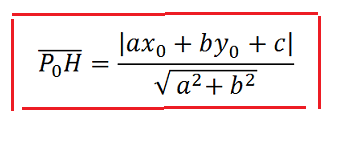
Ad essa siamo giunti usando l'equazione della retta in forma implicita.

ax + by + c = 0.

Ma se volessimo esprimere la DISTANZA di un PUNTO da una RETTA in FORMA ESPLICITA? 

Ricordiamo che l'equazione della retta in forma esplicita è:

y = mx + n.

Per rispondere al nostro quesito basta rammentare che, per passare dalla forma esplicita a quella implicita dell'equazione della retta è sufficiente porre:

m = -a/b

n = -c/b.

Quindi possiamo ricavare dalle relazioni precedenti, rispettivamente i valori di a e di c:

m = -a/b

bm = -a

-bm = a

e

n = -c/b

bn = -c

-bn = c.

Ora sostituiamo, nella formula della DISTANZA di un PUNTO da una RETTA, i valori di a e di c, e avremo:

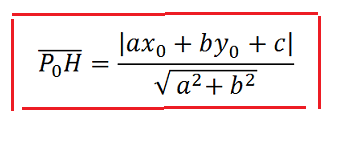
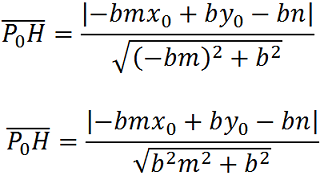
Ora, mettiamo in evidenza, a numeratore e a denominatore la b:

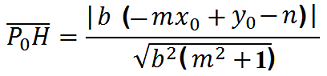
Al denominatore estraiamo la radice quadrata di b² e semplifichiamo:

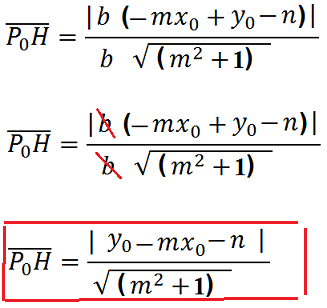
Siamo, così giunti alla formula della DISTANZA di un PUNTO da una RETTA in FORMA ESPLICITA.

Esempio:

determinare la distanza tra il punto P(2; 5) e la retta di equazione 

y = 3x + 2.

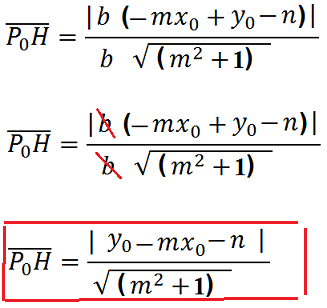
Nel nostro esempio abbiamo che:

x₀ = 2     coordinata X del punto esterno

y₀ = 5     coocrdinata Y del punto esterno

m = 3     coefficente angolare  della retta in forma esplicita

n = 2.      termine noto della retta in forma esplicita

Quindi la formula diventa